|
Como você provavelmente sabe, os transformadores comerciais e os motores elétricos disponíveis comercialmente são enrolados de maneira simétrica, o que os obriga a se opor à sua própria função - um pouco como começar com um carro cuja bateria está esgotada, mas com duas pessoas na frente. frente empurrando para trás e duas pessoas na parte de trás empurrando para a frente. Isso é tão estúpido que é difícil acreditar que alguém faria isso, mas é exatamente assim que motores e transformadores são "projetados" e construídos. Quanto maior a potência de saída, mais a potência de saída se opõe à potência de entrada, o que significa que você precisa ter uma potência de entrada cada vez maior para obter uma saída maior. É disso que trata a lei de Lenz.
Não tem que ser assim. Se você construir um transformador não simétrico como Thane Heins fez, esse efeito está ausente e a potência de saída pode ser quarenta vezes maior do que a potência de entrada, como mostrado pelos resultados dos testes de bancada. Não é tão fácil construir um transformador ou motor completamente não simétrico, mas existem outras maneiras de abordar o problema. Vladimir Utkin produziu a seguinte apresentação explicando os detalhes de uma maneira alternativa de lidar com o problema. Alguns leitores podem achar um pouco técnico nos últimos estágios, mas a informação inicial pode ser entendida por qualquer pessoa. É bem conhecido que as bobinas ortogonais, ou seja, enrolam-se em ângulo reto entre si, não interagem. Isso é ilustrado na Fig.1. Nos diagramas a seguir, a letra “U” representa a tensão, a letra “I” representa corrente e L representa uma bobina de fio:  Fig.1 Essas bobinas ortogonais não interagem Isto significa que quando existe uma voltagem oscilante aplicada à bobina de entrada L1, não há absolutamente nenhuma voltagem induzida na bobina L2. Não faz diferença se as bobinas são de núcleo de ar ou se têm núcleo de ferro. Em outras palavras, pode-se supor que as bobinas são suspensas isoladas no ar. Este é um fato bem conhecido, mas é considerado de pouco interesse, pois é considerado um assunto trivial - não é. Se pudermos fazer com que as bobinas L1 e L2 interajam de modo que a potência real possa ser extraída da bobina L2 sem a potência extraída efetuando a bobina de entrada L1, então essa é uma questão muito diferente e ninguém descartaria isso como sendo “trivial” !! Essa situação muito desejável pode de fato ser realizada como mostrado na Fig. 2, pela adição de dois ímãs permanentes, M1 e M2, um em frente ao outro no eixo da bobina L1, e alternar da bobina de alimentação L1 com tensão para energizá-la com corrente e para isso, adicionamos o capacitor C e operamos a bobina L1 em ressonância onde o campo magnético real está no espaço do ambiente. Aqui, a corrente de entrada está no mínimo e a saída magnética está no máximo. Adicionamos uma carga para bobinar L2, já que agora é capaz de fornecer corrente de saída:  Fig.2 Bobinas ortogonais interagem com simetria quebrada. Na Fig. 2, os pólos sul dos ímãs se enfrentam, mas o arranjo também funciona se for alterado de modo que os pólos norte fiquem frente a frente. Eu sugiro que o problema seja resolvido, isto é, a carga RL recebe energia real, que não tem nenhum impacto na ressonância do circuito de entrada. Agora vou tentar explicar como e por que essa configuração resolve o problema de feedback. A principal explicaçãon Na Fig. 1, quando dois ímanes (M1 e M2), são adicionados como mostrado com os mesmos pólos voltados um para o outro ao longo do eixo da bobina L1, isto adiciona um campo magnético que flui perpendicularmente ao eixo da bobina L1, e engloba alguns, ou todos, da bobina L2. Isso muda tudo, porque as flutuações magnéticas na bobina L1 podem modificar o campo magnético produzido pelos ímãs e provoca tensão e corrente induzidas na bobina L2. Para isso, fizemos o campo magnético "em movimento" adicionando corrente alternada à bobina L1, resultando na passagem alternada do fluxo magnético através da bobina L2. A corrente e a tensão são induzidas na bobina de saída L2. Isto é mostrado na ilustração ligeiramente simplificada Fig. 3, que indica o movimento do campo magnético dependendo se a bobina de alimentação L1 do oscilador aumenta ou se opõe ao campo magnético produzido pelos ímanes permanentes.  Fig. 3. Explicação principal da interação assimétrica das bobinas ortogonais devido ao movimento do campo. A bobina de ressonância L1 é usada para criar um campo magnético oscilante, mas esse campo "em movimento" também pode ser criado usando ímãs permanentes, introduzindo-os no espaço entre dois ímãs opostos através do movimento físico desses ímãs extras, como mostrado na Fig. 4. Os ímãs móveis seriam em um rotor e os pólos dos ímãs do rotor alternariam N, S, N, S…  Fig.4 Explicação do princípio através do uso de ímãs permanentes. Possíveis erros de interpretação Os seguintes erros são possíveis na interpretação das interações descritas: 1. Aproveitar a energia ressonante para a carga. 2. Aproveitando a energia do campo magnético para a carga. Nenhuma interpretação é verdadeira. O princípio básico mostra que a energia de qualquer sistema ressonante não pode ser "explorada" porque isso destruiria a ressonância em si. Além disso, a energia do campo magnético não é usada, porque a magnetização dos ímãs não é alterada ou reduzida de forma alguma. A interpretação mais razoável é a partir da posição de sistemas de energia dupla; dentro do qual, devido à organização interna, alguma energia latente é induzida - e então alimentada à carga. Do ponto de vista de um observador externo (o oscilador), essa energia é imaginária, mas em termos de um observador interno (a bobina de saída) é bastante real. Monitorar a energia em diferentes sistemas de coordenadas produz resultados diferentes, que estão em conformidade com o conhecimento científico atual. A Lei da Conservação da Energia O teorema de 1918 do matemático Emma Noether afirma que cada simetria contínua de um sistema físico corresponde a uma lei de conservação: Simetrias de tempo correspondem à lei de conservação de energia, Simetrias de espaço correspondem à lei da conservação do momento, A isotropia do espaço corresponde à lei de conservação do momento angular, A simetria de medida corresponde à lei de conservação de carga elétrica e assim por diante. Ou seja, a simetria existe na natureza, e então isso leva à teoria da lei de conservação correspondente. Ao mesmo tempo, todas as simetrias são vistas como "imutáveis". A possibilidade de quebrar qualquer simetria não é sequer considerada, embora fazer isso não contradiz realmente nada, apenas muda a física. Assim, a Lei da Conservação da Energia, na verdade, não pode ser violada como princípio, porque essa “Lei” é o resultado de uma interação simétrica existente e não a causa dessa interação simétrica. No entanto, para contornar a aplicabilidade da Lei de Conservação de Energia é perfeitamente possível. Para fazer isso, tudo o que é necessário é organizar as coisas de maneira a quebrar a simetria. O método descrito acima é uma interação assimétrica, e o teorema de Emma Noether simplesmente não se aplica (mas isso precisa ser provado em uma data futura). A dependência do poder de saída A potência de saída depende de vários parâmetros: 1. Em primeiro lugar, depende da intensidade do campo magnético inicial dos ímãs permanentes, que deve ser "movido". Quanto maior a intensidade desse campo magnético, maior será a potência de saída. Um campo magnético de intensidade zero produz saída zero. 2. Em segundo lugar, depende da distância através da qual o campo magnético inicial se desloca, isto é, da corrente na bobina ressonante (ou, mais precisamente, da potência reativa causada por esse fluxo de corrente). 3. Em terceiro lugar, depende da velocidade de "movimento" do campo magnético inicial, isto é, da frequência de ressonância. Quanto maior a frequência, maior será a potência de saída, porque a bobina de saída EMF depende da velocidade das alterações no campo magnético inicial. Este último ponto sugere a diminuição da capacitância do circuito ressonante, quando a tensão nele é aumentada (para preservação da energia armazenada no circuito). Isso deve levar ao aumento da potência de saída. Substituindo os ímãs permanentes por eletroímãs A substituição de ímãs permanentes por eletroímãs é óbvia e pode ser feita por várias razões. Por exemplo, pode ser devido à falta dos magnetos permanentes necessários, ou alternativamente, devido ao fato de que os ímãs se tornam gradualmente desmagnetizados devido à influência do "campo móvel" da bobina L1. De qualquer forma, a substituição de eletroímãs definitivamente pode ser feita. Fazemos isso para a generalização do princípio, porque mais tarde mostraremos que os eletroímãs foram usados em alguns dispositivos de "arte prévia". Neste caso, os eletroímãs podem ser incluídos sequencialmente ou em paralelo, a polaridade da tensão aplicada a eles também pode ser selecionada arbitrariamente. Uma dessas modificações é mostrada na Fig. 5 para eletroímãs sequenciais (A) e (B) paralelos  Fig. 5. Substituindo os ímãs permanentes por eletroímãs com (A) serial e (B) conexão paralela. Aqui, para conexão paralela do par de eletroímãs, pode ser representado como uma bobina de curto-circuito, na qual a bobina ressonante induz a tensão da seguinte distribuição:  Fig.6 A bobina ressonante induzida por tensão em eletroímãs incluídos em paralelo. Isto permite que a bobina de saída seja colocada no mesmo eixo que a bobina ressonante, porque a bobina ressonante não induz tensão na bobina de saída sem corrente nos eletroímãs. Na prática, isso faz com que a bobina ressonante seja enrolada exatamente na metade do curto-circuito e a bobina de saída na posição correta da bobina de curto-circuito. Usando o efeito eletro-radiante Usar o efeito eletro-radiante é uma extensão da ideia de usar ímãs ao causar interação entre bobinas ortogonais. O objetivo é a eliminação do oscilador mestre e da fonte de alimentação dos eletroímãs. A maneira mais fácil de ver o efeito eletro radiante é com a descarga de faísca de um capacitor pré-carregado, onde pelo menos um de seus eletrodos é um indutor.  Fig.7 A manifestação mais simples do efeito eletro-radiante (a luz está acesa). Estamos interessados na opção (B), na qual uma placa é totalmente enrolada em uma direção e o outro eletrodo é feito em duas metades enroladas em direções opostas. O eletrodo é enrolado em uma direção, será usado como bobina ressonante e uma placa de duas metades como os enrolamentos dos solenóides. O resultado desta modificação é apresentado na Fig. 8 para os solenóides de alimentação seriais (A) e paralelos (B). Se o fluxo de faíscas (descarga de capacitância turn-to-turn) ocorrer com uma frequência do circuito de ressonância, isso levará à manutenção de oscilações sustentadas no circuito da bobina. O que você precisa para "mover" o campo magnético. E os solenóides (eletroímãs) seriam para criar uma corrente, necessária para garantir os campos iniciais que você deseja “mover”. Assim, um gerador separado para ressonância e uma fonte separada de corrente para os solenóides não é necessário. A faísca será fraca, pois não comuta nenhum circuito de alta corrente. 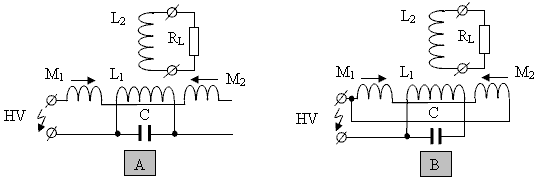 Fig. 8. O uso do efeito eletro-radiante para manter a ressonância e criar uma corrente nos solenóides (eletroímãs) em seus arranjos seqüenciais (A) e paralelos (B). Íman poderoso - frequência de ressonância de zero Esta abordagem é uma continuação das idéias de solenóides e efeito elétrico-radiante. Electro - O efeito de aquecimento por baixo do piso é permitido para se livrar do gerador e uma fonte de alimentação separada para os solenóides, para criar um poderoso campo magnético alternado para mover a bobina ressonante (com frequência de fornecimento de faísca apropriada). No entanto, o campo magnético inicial nos solenóides pode ser bastante fraco. Para fortalecê-lo, e criar um poderoso ímã permanente, usou a idéia de "ressonância na freqüência zero" ou acumulação de corrente - Fig. 8 (A).  Fig. 8(A) Ilustração da ideia de "frequência de ressonância zero" ou a acumulação atual. Essa idéia é bastante simples e consiste no diodo de capacitância inter-voltas de descarga nos solenóides de shunt - Fig. 8 (A). O diodo é usado para manter a corrente nos solenóides entre a capacitância entre descargas. Cada capacitância inter-turn de descarga, a corrente nos solenóides é aumentada (de acordo com a lei de conservação de energia) e aumenta a potência de saída de todo o dispositivo. O aumento na corrente (e potência) ocorrerá enquanto as perdas nos solenóides forem iguais à energia de entrada devido à capacitância inter-voltas de descarga. Circuitos de comutação shunt para acumular diodos de corrente, em série (A) e uma conexão paralela de bobinas (B) são mostrados na Fig. 8 (B).  Fig. 8(B) Esquema que incorpora díodos de derivação para acumular corrente, em série (A) e a conexão paralela de bobinas (B). Essa abordagem permite "espremer" o efeito eletro-radiante de quase tudo, ou seja, o poderoso eletroímã ressonante da bobina, solenóide. ATENÇÃO: Esquemas de solenóides de derivação para dispositivos específicos podem variar ligeiramente (por exemplo, aterrando as bobinas do ponto central). Usando os eletroímãs como uma bobina de saída Essa abordagem é uma continuação para idéias de eletromagnetos e o efeito eletro-radiante. Seria interessante não usar a bobina de saída e usar os eletroímãs para ela, garantindo assim a interação das duas bobinas ortogonais. Nesse caso, a criação de um campo inicial (para "mover") e a coleta de energia de saída são obtidas pelos mesmos elementos de circuito. Para fazer isso, você precisa organizar as coisas de modo que o campo magnético "em movimento" "pressione" diferentemente para cada um dos eletroímãs, levando à formação neles de diferentes correntes. Para este fim, os eletroímãs conectados em série podem ser desviados pelo capacitor e conectados em paralelo com os eletroímãs usados, mas com um número de voltas um pouco diferente. A distribuição de tensão resultante no eletroímã comum será alterada.  Fig. 9. Uma distribuição de tensão comum nos eletroímãs (A) e quando eles são usados como bobina de saída (B). 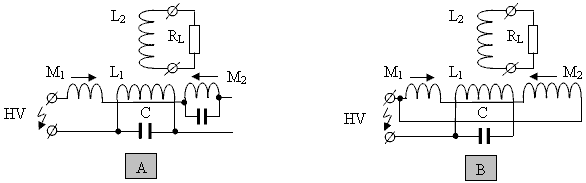 Fig. 10. Usando eletroímãs assimétricos como bobina de saída. Mas, o uso de eletroímãs simétricos também é possível. "Desmagnetização" - amplificação de corrente "Desmagnetização" ou "troca de fluxo magnético" é um tipo de interação assimétrica para bobinas ortogonais. Para as duas bobinas interagirem, é necessário criar um campo magnético inicial. A implementação mais simples do esquema "desmagnetização" é baseada em núcleos ferromagnéticos em forma de E e é como segue. A bobina que cria o campo magnético original é enrolada no topo do núcleo do tipo E. A bobina de desmagnetização é enrolada no núcleo como de costume, como mostrado na Fig.10. Na ausência de corrente na bobina externa e na ausência de corrente na bobina interna, elas não interagem - a saída EMF na bobina externa é zero - Fig.10 (A). Se houver uma corrente na bobina externa e uma corrente fornecida à bobina interna, o fluxo magnético no núcleo ferromagnético está tentando fechar o fluxo magnético externo em si mesmo. Um campo magnético externo começa a "desaparecer". Como resultado, a corrente na bobina externa está aumentando para compensar o campo magnético "desaparecido" - Fig. 10 (B).  Fig. 11. Um esquema simples de "desmagnetização" baseado em núcleos em forma de E. 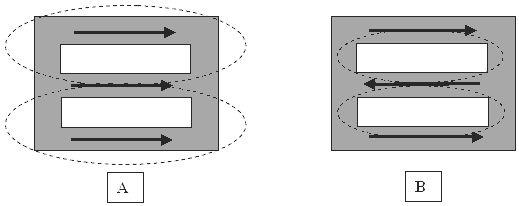 Fig. 12. A direção do campo magnético dentro do ferromagnético núcleo para magnetização - (A) e desmagnetização - (B). A potência de saída depende dos mesmos fatores mencionados anteriormente. Não há interação sem o campo magnético inicial. Circuitos de interação descritos anteriormente sem uma bobina de saída dividida também podem ser considerados uma forma do princípio de "desmagnetização" ou ganho de corrente. Esquemas já conhecidos Os circuitos mais conhecidos são das apresentações de Donald Smith e principalmente seu documento em PDF. Seu circuito mais simples é composto por uma bobina ressonante e uma bobina de saída, e os eletroímãs são usados em conexão paralela em vez de ímãs. Um efeito eletro-radiante é usado para excitação.  Fig. 13. Esquema do documento de Donald Smith.  Fig. 14. Distribuição de tensão no eletroímã (7) a partir da ação do bobina ressonante (6) e a ação da corrente de alimentação inicial através o resistor (8). Figuras (1) e (2) respectivamente. Pode ser claramente visto na Fig. 14 que a bobina de saída 6 (A) não interage com a bobina ressonante "em movimento" de entrada (6) e não afeta a ressonância. Um análogo elétrico do esquema de Donald Smith sem usar o efeito eletro-radiante é mostrado na Fig. 15.  Fig. 15. Análogo elétrico do dispositivo de Donald Smith, sem usar o efeito eletro-radiante (usando a mesma notação do original). Outro esquema de Donald Smith usa eletromagnetos em vez de uma única bobina de saída. Para poder usar eletroímãs (7) como bobina de saída, eles são assimétricos. Tudo o resto é semelhante.  Fig. 16. Esquema do documento de Donald Smith. Um análogo elétrico do esquema de Donald Smith sem usar o efeito eletro-radiante é mostrado na Fig. 17:  Fig. 17. Análogo elétrico do dispositivo de Donald Smith, sem usar o efeito eletro-radiante (usando a mesma notação do original) E, mais um esquema do dispositivo de Don Smith é mostrado aqui na Fig. 18. Ele tem alguns erros, mas esses não são importantes para entender o processo. Neste caso, os solenóides são conectados em série, e o efeito eletrorradiante é usado para excitação da corrente inicial neles.  Fig. 18. Esquema do documento de Donald Smith com serialmente eletroímãs conectados e excitação eletro-radiante.  Fig. 19. Análogo elétrico do dispositivo de Donald Smith, sem usar o efeito eletro-radiante. E finalmente, o dispositivo eletromecânico de Donald Smith - (A), e seu possível esquema - (B) na Fig. 20.  Fig. 20. TO dispositivo eletromecânico de Donald Smith (A) e seu possível esquema (B) A presença do campo magnético original é um fator importante nos dispositivos de "energia livre", baseado na interação das bobinas ortogonais (um transformador assimétrico). Não há interação entre as bobinas sem o campo magnético inicial. Este campo magnético inicial pode ser criado por ímãs permanentes ou eletroímãs (possivelmente envolvendo o efeito eletro-radiante). Como um caso especial, este campo pode ser criado pela corrente inicial na bobina de saída. O que leva ao esquema de "desmagnetização" ("deslocamento, movimento") com o aumento da corrente inicial. Aqui, uma corrente de "movimento, comutação e desmagnetização" é usada como a corrente ressonante necessária para a bobina de entrada. A este respeito, podemos lembrar as palavras de Donald Smith, quando ele diz que o campo magnético é a força primária no eletromagnetismo. O significado de suas palavras fica claro, a saber, que sem o campo magnético inicial, não há interação entre as bobinas ortogonais. O efeito descrito aqui é conhecido há muitas décadas e tem sido usado por muitos pesquisadores da "energia livre" para criar seus próprios dispositivos. Eles foram independentemente "inventando e reinventando" o efeito. No entanto, há uma razão para acreditar que a primeira vez que foi usada foi com o estudo do transformador ressonante de Nikola Tesla (com excitação por faísca). Além disso, dado no esquema, pode-se entregar outros esquemas e fotografias dos vários circuitos e dispositivos (elétricos e eletromecânicos), de uma ampla variedade de autores, no entanto, este trabalho não se destina a ser uma enciclopédia. Em vez disso, vamos nos lembrar mais uma vez: 1. Lei de conservação de energia é o resultado (não o motivo) da interação simétrica. 2. A maneira mais fácil de destruir a interação equilibrada - para usar um feedback eletromagnético no campo. 3. Todos os sistemas assimétricos estão fora da área especificada na lei de conservação de energia. 4. A Lei de Conservação de Energia não pode ser quebrada, mas só se aplica a interações simétricas. Nenhum segredo particular ou de estado está contido neste documento, que usa somente material de código aberto. Por favor, note que todos os gráficos e diagramas são fornecidos apenas como uma ajuda aos princípios. Nossos agradecimentos vão para Vladimir Utkin por compartilhar livremente esta informação importante. Patrick Kelly http://www.free-energy-info.tuks.nl http://www.free-energy-info.com http://www.free-energy-info.co.uk http://www.free-energy-devices.com engpjk (at) gmail (dot) com |