 INTRODUCTION It’s well known, that orthogonal coils, that is, coils at right angles to each other, do not interact. This is illustrated in Fig.1. In the following diagrams, the letter “U” represents voltage, the letter “I” represents current and L stands for a coil of wire:  Fig.1 These orthogonal coils do not interact This means that when there is an oscillating voltage applied to the input coil L1, there is absolutely no voltage induced in the coil L2. It makes no difference if the coils are air-core or if they have an iron core. In other words, it can be assumed that the coils are suspended isolated in air. This is a well-known fact but it is considered to be of little interest as it is thought to be a trivial matter – it isn’t. If we can make the coils L1 and L2 interact so that real power can be extracted from coil L2 without that extracted power effecting the input coil L1, then that is a very different matter and nobody would dismiss that as being “trivial” !! That very desirable situation can indeed be brought about as shown in Fig.2, by adding two permanent magnets, M1 and M2, facing each other on the axis of the coil L1, and switch from powering coil L1 with voltage to powering it with current, and for that, we add the capacitor C and operate coil L1 in resonance where the real magnetic field is in the ambient space. Here, the input current is at a minimum and the magnetic output is at its maximum. We add a load to coil L2 as it is now able to provide output current:  Fig.2 Orthogonal coils interact with broken symmetry. In Fig.2 the South poles of the magnets face each other, but the arrangement also works if it altered so that the North poles face each other. I suggest that the problem is solved, that is, the load RL receives real power, which has no bearing on the resonance of the input circuit. I will now try to explain how and why this configuration solves the feedback problem. In Fig. 1, when two magnets (M1 and M2), are added as shown with the same poles facing each other along the axis of the coil L1, this adds a magnetic field which flows perpendicular to the axis of coil L1, and encompasses some, or all, of coil L2. This changes everything, because the magnetic fluctuations in coil L1 can modify the magnetic field produced by the magnets and causes induced voltage and current in coil L2. For this, we made the "moving" magnetic field by adding alternating current to the coil L1, resulting in alternating magnetic flux passing through coil L2. Current and voltage are induced in the output coil L2. This is shown in the slightly simplified illustration Fig. 3, indicating the movement of the magnetic field depending on whether or not the oscillator powering coil L1 augments or opposes the magnetic field produced by the permanent magnets.  Fig. 3. Principle explanation of the asymmetrical interaction of the orthogonal coils due to the movement of the field. The resonance coil L1 is used to create an oscillating magnetic field, but that "moving" field can also be created using permanent magnets, introducing them into the gap between two oppositely facing magnets through the physical movement of those extra magnets as shown in Fig. 4. The moving magnets would be on a rotor and the poles of the rotor magnets would alternate N, S, N, S…  Fig.4 Explanation of the principle through the use of permanent magnets. The following errors are possible in the interpretation of the described interactions: 1. Harnessing resonant energy to the load. 2. Harnessing the magnetic field energy to the load. Neither interpretation is true. The basic principle shows that the energy of any resonant system cannot "be tapped" because doing that would destroy the resonance itself. Also, the energy of the magnetic field is not used, because the magnetisation of the magnets is not changed or reduced in any way. The most reasonable interpretation is from the position of double energy systems; within which, due to internal organisation, some latent energy is induced - and then fed to the load. From the point of view an outside observer (the oscillator), this energy is imaginary, but in terms of an internal observer (the output coil) it is quite real. Monitoring the energy in different coordinate systems produces different results, which conform to the current scientific knowledge. The 1918 theorem of the mathematician Emma Noether states, that each continuous symmetry of a physical system corresponds a conservation law: Symmetries of time corresponds to the law of conservation of energy, Symmetries of space corresponds to the law of conservation of momentum, Isotropy of space corresponds to the law of conservation of angular momentum, Gauge symmetry corresponds to the law of conservation of electric charge, and so on. That is, the symmetry exists in Nature, and then that leads to the corresponding Conservation Law theory. At the same time, all the symmetries are seen as "immutable". The possibility of breaking any symmetry is not even considered, although doing that does not actually contradict anything, it merely changes the physics. Thus, the Law of Conservation of Energy actually cannot be violated as a principle, because that “Law” is the result of an existing symmetrical interaction and not the cause of that symmetrical interaction. However, to bypass the applicability of the Law of Conservation of Energy is perfectly possible. To do that, all that is needed is to arrange things in such a way that it breaks the symmetry. The method described above is an asymmetrical interaction, and Emma Noether's theorem just does not apply (but, that needs to be proved at a future date). The output power depends on several parameters: 1. First of all, it depends on the intensity of the initial magnetic field of the permanent magnets, which is to be "moved". The greater the intensity of that magnetic field, the higher the output power will be. A zero intensity magnetic field produces zero output. 2. Secondly, it depends on the distance through which the initial magnetic field shifts, that is, from the current in the resonant coil (or more accurately, on the reactive power caused by that current flow). 3. Thirdly, it depends on the speed of "movement" of the initial magnetic field, that is, from the resonant frequency. The higher the frequency, the higher the output power will be, because the EMF output coil depends on the speed of changes in the initial magnetic field. This last point suggests the decrease of resonant circuit capacitance, when the voltage on it is raised (for preservation of the stored energy in the circuit). This should lead to increased output power. Replacement of permanent magnets by electromagnets is obvious and may be done for various reasons. For example, it could be due to lack of the necessary permanent magnets, or alternatively, due to the fact that magnets become gradually demagnetised due to the influence of "moving field" of L1 coil. Anyway, the substitution of electromagnets can definitely be done. We do this for the generalisation of the principle, because later we will show that electromagnets were used in some ‘prior art’ devices. In this case the electromagnets can be included either sequentially or in parallel, the polarity of voltage applied to them can also be selected arbitrarily. One such modification is shown in Fig, 5 for (A) sequential and (B) parallel electromagnets.  Fig. 5. Replacing the permanent magnets by electromagnets with (A) serial and (B) parallel connection. Here, for parallel connection of the pair of electromagnets, it can actually be represented as one short-circuited coil, in which the resonant coil induces the voltage of the following distribution:  Fig.6 The voltage induced resonant coil in electromagnets included in parallel. This allows the output coil to be placed on the same axis as the resonant coil, because the resonant coil induces no voltage in the output coil without current in the electromagnets. In practice, this leads to the resonant coil being wound exactly halfway of the short-circuited, and the output coil in the correct position of the short-circuited coil. Using the electro-radiant effect is an extension of the idea of using magnets when causing interaction between orthogonal coils. The purpose is the elimination of the master oscillator and power supply for the electromagnets. The easiest way to see the electro-radiant effect is with the spark discharge of a pre-charged capacitor, where at least one of its electrodes is an inductor  Fig.7 The simplest manifestation of the electro-radiant effect (the light is on). We are interested in option (B), in which one plate is fully wound in one direction and the other electrode is made in two halves wound in opposite directions. The electrode is wound in one direction, will be used as the resonant coil, and a plate of two halves as the windings of the solenoids. The result of this modification is presented in Fig.8 for serial (A) and parallel (B) powering solenoids. If the flow of sparks (inter-turn capacitance discharge) occurs with a frequency of the resonance circuit, it will lead to the maintenance of sustained oscillations in the coil circuit. What you need to “move” the magnetic field. And the solenoids (electromagnets) would be to create a current, necessary to ensure initial fields that you want to “move”. Thus, a separate generator for resonance and a separate source of current for the solenoids is not required. The spark will be weak, since it does not commute any high current circuits..  Fig. 8. Usage of the electro-radiant effect to maintain resonance and to create a current in the electromagnets in their serial (A) and parallel (B) connections. This approach is a continuation of the ideas of solenoids and electric-radiant effect. Electro - Under floor heating effect is allowed to get rid of the generator and a separate power supply for the solenoids, to create a powerful alternating magnetic field to move the resonant coil (with appropriate spark supply frequency). However, the initial magnetic field in the solenoids can be quite weak. To strengthen it, and create a powerful permanent magnet used the idea of "resonance at zero frequency" or current accumulation – Fig. 8 (A).  Fig. 8(A) Illustration of the idea of "zero resonance frequency" or the accumulation of current. This idea is quite simple and consists in the discharge inter-turn capacitance diode in the shunt solenoids - Fig. 8 (A). The diode is used to maintain the current in the solenoids between discharges inter-turn capacitance. Each discharge inter-turn capacitance, the current in the solenoids is increased (in accordance with the energy conservation law), and increases the power output of the entire device. The increase in current (and power) will occur as long as the losses in the solenoids are equal to the input energy due to discharge inter-turn capacitance. Shunt switching circuits for accumulating current diodes, in serial (A) and a parallel connection of coils (B) are shown in Fig. 8 (B).  Fig. 8(B) Scheme incorporating bypass diodes to accumulate current, in serial (A) and the parallel connection of coils (B). This approach allows you to "squeeze out" of the electro-radiant effect almost everything, that is, the coil - resonant, solenoids - powerful electromagnet. ATTENTION: Schemes shunt solenoids for specific devices may vary slightly (e.g., by grounding the middle point coils). This approach is a continuation for electromagnets ideas and the electro-radiant effect. It would be interesting not to use the output coil and use the electromagnets for it, thus ensuring the interaction of the two orthogonal coils. In this case, the creation of an initial field (for "moving") and harvesting output energy are achieved by the same circuit elements. To do this, you need to arrange things so that the "moving" magnetic field "presses" differently for each of the electromagnets, leading to the formation in them of different currents. To this end, electromagnets which are connected in series can be shunted by capacitor, and connected in parallel with the electromagnets used but with a somewhat different number of turns. The resulting voltage distribution on the common electromagnet will be changed.  Fig. 9. An ordinary voltage distribution on the electromagnets (A) and when they are used as an output coil (B). 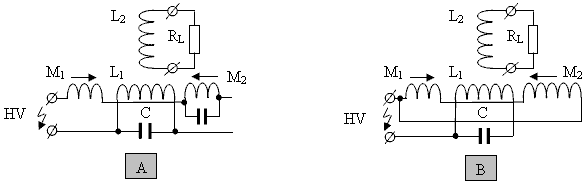 Fig. 10. Using asymmetrical electromagnets as an output coil. But, the use of symmetrical electromagnets is also possible. "Demagnetisation" or "switching magnetic flux" is a kind of asymmetrical interaction for orthogonal coils. For the two coils to interact one needs to create an initial magnetic field. The simplest implementation of the scheme "demagnetisation" is based on E-shape ferromagnetic cores and is as follows. The coil which creates the original magnetic field, is wound on top of the E - type core. The demagnetising coil is wound on core as usual as shown in Fig.10. In the absence of current in the outer coil and the absence of current in the inner coil, they do not interact - the output EMF on the external coil is zero - Fig.10 (A). If there is a current in the outer coil, and a current supplied to the inner coil, the magnetic flux in the ferromagnetic core is trying to close the external magnetic flux on itself. An external magnetic field begins to "fade". As a result, the current in the outer coil is increasing to compensate the "disappearing" magnetic field – Fig. 10 (B).  Fig. 11. A simple "demagnetisation" schematic based on E-shaped cores. 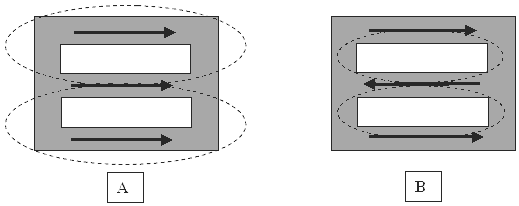 Fig. 12. The direction of the magnetic field inside the ferromagnetic core for magnetisation - (A) and demagnetisation - (B). The output power depends on the same factors as mentioned earlier. There is no interaction without the initial magnetic field. Previously described interaction circuits without a divided output coil can also be considered a form of the principle of "demagnetisation" or current gain. The best known circuits are from Donald Smith’s presentations and mainly his pdf document. His most simple circuit is comprised of a resonant coil and an output coil, and electromagnets are used in parallel connection instead of magnets. An electro-radiant effect is used for excitation.  Fig. 13. Schematic from Donald Smith’s document.  Fig. 14. Voltage distribution on the electromagnet (7) from the action of the resonant coil (6) and the action of initial powering current through the resistor (8). Figures (1) and (2) respectively. It can be clearly seen from Fig.14 that the output coil 6 (A) does not interact with the input "moving" resonant coil (6) and does not affect resonance. An electrical analogue of Donald Smith's schematic without using the electro-radiant effect is shown in Fig. 15.  Fig. 15. Electrical analogue of Donald Smith’s device, without using the electro-radiant effect (using the same notation as the original). Another of Donald Smith's schematics uses electromagnets instead of a single output coil. To be able to use electromagnets (7) as the output coil, they are made asymmetrical. Everything else is similar.  Fig. 16. Schematic from the Donald Smith document. An electrical analogue of the Donald Smith's schematic without using the electro-radiant effect is shown in Fig. 17:  Fig. 17. Electrical analogue of Donald Smith’s device, without using the electro-radiant effect (using the same notation as the original). And, one more schematic of Don Smith device is shown here in Fig. 18. It has some errors, but those are not important for understanding the process. In this case, the solenoids are connected in series, and the electro–radiant effect is used for excitation of the initial current in them.  Fig. 18. Schematic from the Donald Smith document with serially connected electromagnets and electro–radiant excitation.  Fig. 19. Electrical analogue of the Donald Smith’s device, without using the electro-radiant effect. And finally, the electro–mechanical device from Donald Smith - (A), and its possible schematic - (B) in Fig. 20.  Fig. 20. The electro–mechanical device from Donald Smith (A) and its possible schematic (B) The presence of the original magnetic field is an important factor in the devices of "free energy", based on the interaction of the orthogonal coils (an asymmetrical transformer). There is no interaction between the coils without the initial magnetic field. This initial magnetic field can be created either by permanent magnets or electromagnets (possibly involving the electro-radiant effect). As a special case, this field can be created by the initial current in the output coil. Which leads to the schematic of "degaussing" ("shifting, moving") with increasing initial current. Here, a "moving, switching, demagnetisation" current is used as the resonant current needed by the input coil. In this regard, we can recall the words of Donald Smith, when he says that the magnetic field is the primary force in electromagnetism. The meaning of his words become clear, namely that without the initial magnetic field, there is no interaction between orthogonal coils. The effect described here has been known for many decades and has been used by many "free energy" researchers to create their own devices. They were independently "inventing and reinventing" the effect. However, there is a reason to believe that the first time it was used was with Nikola Tesla’s resonant transformer study (with spark excitation). Also, given in the schematics, one could deliver other schematics and photographs of the various circuits and devices (both electrical and electromechanical), from a wide variety of authors, however, this work is not intended to be an encyclopaedia. Instead, let us recall once again: 1. Energy conservation law is the result (not the reason) of symmetric interaction. 2. The easiest way to destroy the balanced interaction - to use an electromagnetic feedback in the field. 3. All asymmetrical systems are outside the area specified in the energy conservation law. 4. The Law of Conservation of Energy cannot be broken but it only applies to symmetrical interactions. Patrick Kelly http://www.free-energy-info.tuks.nl http://www.free-energy-info.com http://www.free-energy-info.co.uk http://www.free-energy-devices.com engpjk (at) gmail (dot) com |